発振回路についての記事になります。
たまごっちなどおもちゃの制御ICの外付け発振回路に付いている32.768kHzのクリスタルをご存じかとは思います。
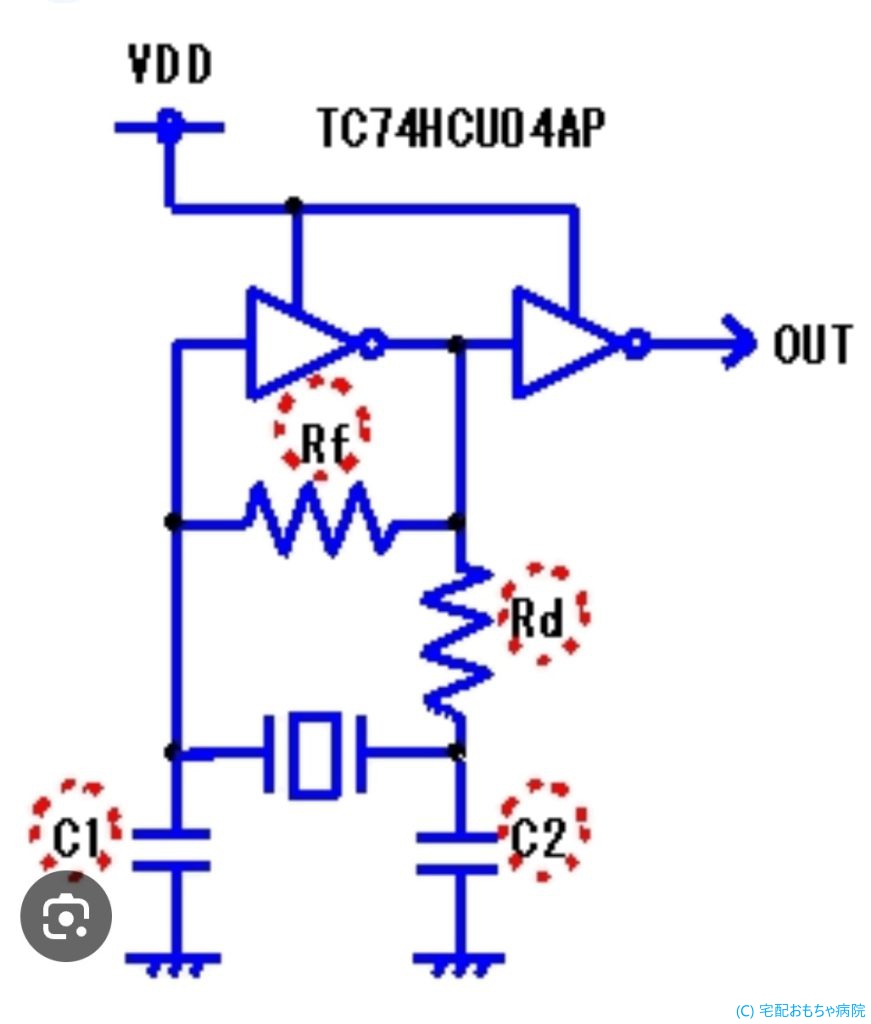
マイコンなどの製品開発の経験などあれば、基礎知識として発振回路やIC内部のPLL回路などでこれらクリスタルの役目や回路仕様も把握していなければなりません。
もちろんですが、おもちゃ修理に関しても必須事項です。
車載マイコンの設計や開発をしていました頃は、品質や信頼性などたいへん厳しい要件があり検証や評価をしていたころをよく思いだします。
外付けの発振回路は、それぞれの回路の応じた品質や信頼性の検証や評価の基で設計されます。
電源、温度、部品のバラつき、基板の誘電率などなど。
さて、話を32.768kHzのクリスタルに戻します。
当医院の記事でもよく登場しますが、時計など時を刻む場合、よく目にするシリンダー型の32.768kHzのクリスタルを目にします。
で、なぜ時を刻むのに32.768kHzのクリスタルなのか?
と思ったことありませんか?
マイコン設計やデジタル回路の設計経験があれば、既にご存じかと思いますが、それは、インプリが容易だからです。
実現しようとすれば、他のクリスタルでも時を刻むことはできますが、32.768kHzですと容易になります。
皆さん、分かりますか?
理工系の学生さんであれば宿題にすべきところですが、答えはカウンターなどで容易に実現できるからです。
32.768kHzって何Hzですか?
32.768kHz = 32768Hz
1秒に32768回振動します。
これって、いいかえると、32768回の振動で1秒とも言えます。
発振子が、計測開始から32768回振動した時が1秒であると言えることになります。
この32768回というのがみそです。
他の周波数であれば、それぞれの回数カウントすればいいのですが、この32768回は、1秒を2の15乗の分周比で実現できます。※電卓で2を押し、×を2度押して、=を繰り返し押してみてください。14回目で32768になるでしょ?
ん?分周ってなに?という方は工学系の教養の書籍などで調べてみてください。
デジタル回路のお話になってしまうのですが、2の4乗、すなわち16bitのカウンターなど多用します。Verilogなんかでは簡単に記述でき、合成でも問題なく論理合成もできます。
もう、今現在はそんなことはしていなさそうですが、私が現役のころは、VerilogでHDLを記述しDesign Compilerで合成など懐かしい言葉となります。
巷では、AIで論理合成/配置配線が一括でGDSまで吐いてくれるそうです。時代も進んでおりますね、、、。
EDAベンダーさんには、エンジニア時代の諸先輩方が多くおられたのですが、皆さんお元気でしょうか?
さて、話をカウンターに戻すと16bitのカウンターであれば、
10進の32768という値は、2進では、1000_0000_0000_0000と表現でき、つまり2の15乗であります。
刻々をカウンターをクリスタルの発振の立ち上げか立下りのエッジでインクリメントした場合、ちょうど15bit目のインクリメントで1秒を刻めます。
例えば、FF(フリフロ)で実現されたカウンターのCKinに印加したイメージです。


